Covid-19: Schlimmer als Influenza? Eine GedankenübungLesezeit: 6 Minuten
Strategic Intelligence – Bildquelle: Screenshot-Ausschnitt intelligence.weforum.org
Vorbemerkung:
Das Nachfolgende ist eine reine Gedankenübung – ohne Anspruch auf Vollständigkeit oder Fehlerfreiheit. Es kann durchaus sein, das ich an einer Stelle einmal falsch abgebogen bin, da das Thema doch durchaus komplex ist. Daher bitte ich um entsprechende Prüfung. Und bekanntlich kann man ja jede Statistik zum eigenen Weltbild passend modellieren. Datengrundlage für die hier angestellten Berechnungen sind die verfügbaren Angaben zum 24. März 2020.
Das Robert-Koch-Institut (RKI) gibt wöchentlich den sogenannten Influenza-Wochenbericht heraus, in dem die vorhandenen Fallzahlen zu den Influenza A(H1N1)pdm09-, Influenza A(H3N2)- und Influenza B-Viren aufgeführt werden.
Im derzeit aktuellen Wochenbericht zur Kalenderwoche 11/2020 finden wir auf Seite 6 die Meldedaten nach dem Infektionsschutzgesetz (IfSG) der Meldewochen 6 bis 11 – also der Zeitraum, der auch bei der Erhebung von Covid-19 aktuell herangezogen wird.
In diesem Meldezeitraum von sechs Wochen wurden insgesamt 127.263 Influenza-Meldungen (MW 6 bis 11) an das RKI übermittelt.
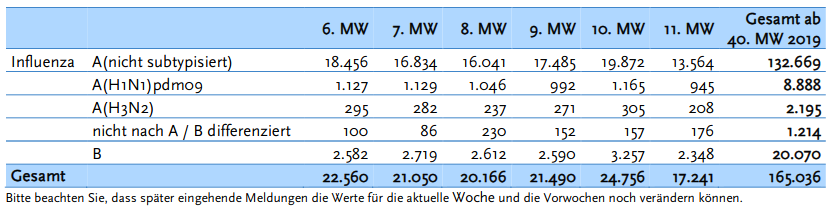
Influenza Meldewoche 6-11 – Bildquelle: Screenshot-Ausschnitt PDF
Zudem gibt das RKI jedes Jahr einen Saisonbericht zur Influenza heraus. Letztmalig für die Saison 2018/2019.
In diesem Bericht finden wir auf Seite 35 die Gesamtanzahl der an das RKI gemäß IfSG in der Saison 2018/19 übermittelten labordiagnostisch bestätigten Influenza-Fälle. Diese betrug im Berichtszeitraum 181.105 Personen, wovon 852 nach den offiziellen Rückmeldungen verstorben sind.
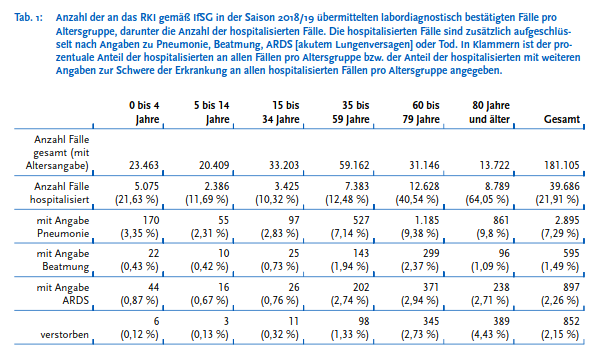
Influenza-Fälle 2018-2019 – Bildquelle: Screenshot-Ausschnitt PDF
Dabei ist jedoch zu sagen, dass diese 852 Todesfälle für eine klassische Aussage zur Todesrate der Influenza-Viren ungeeignet ist. So schreibt das RKI auf Seite 46 unter dem Punkt 5.3. Influenza-bedingte Todesfälle (Exzess-Schätzungen):

Influenza-bedingte Todesfälle Seite 46 – Bildquelle: Screenshot-Ausschnitt PDF
Daher wird eine sogeannnte Exzess-Schätzung vorgenommen. Diese im Bericht auf Seite 47 zu findende Schätzung besagt, dass in der Saison 2017/18 ca. 25.100 Menschen an Influenza gestorben sind (für 2018/2019 liegen noch keine Daten vor):
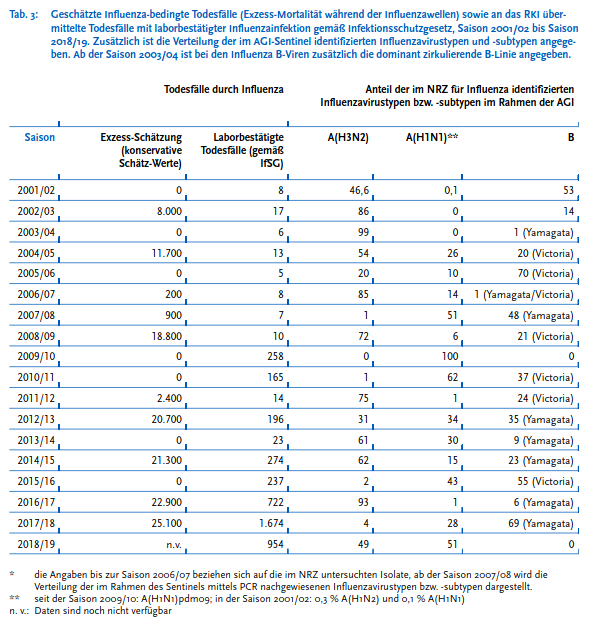
Influenza Exzess-Schätzung – Bildquelle: Screenshot-Ausschnitt PDF
Nehmen wir die weiter oben aufgeführten Influenza-Erkrankten von 181.105 und setzen diese ins Verhältnis zu den 25.100 Verstorbenen, ergibt sich eine Todesrate von 13,86. Da aber genauso die Begründung für die Exzess-Schätzung auch für die gemeldeten Influenza-Rückmeldungen gelten muss (schließlich geht nicht jeder direkt zum Arzt und wird dadurch erfasst), nehmen wir die offiziellen, in der obigen Grafik aufgeführten 1.674 laborbestätigten Todesfälle und setzen diese ins Verhältnis zu den eingemeldeten Influenza-Fällen von 181.105. Hier erhalten wir ein Verhältnis von 0,92.
Kommen wir noch einmal auf den Bildausschnitt Influenza der Meldewochen 6 bis 11 zurück:

Influenza Meldewoche 6-11 – Bildquelle: Screenshot-Ausschnitt PDF
Insgesamt haben sich in diesem Zeitraum 127.263 Menschen mit Influenza infiziert. Berechnen wir die zu erwartende Anzahl von Sterbefällen mit den weiter oben berechneten Verhältnis von 0,92, bedeutet dies, dass in diesem Berichtszeitraum rechnerisch gesehen 1.170 Menschen an der Influenza verstorben sind.
Da jedoch der Verhältniswert von 0,92 das ganze Jahr (und bekanntlich sind im Sommer die Zahlen deutlich geringer) berücksichtigt, wollen wir nur den im Bericht erwähnten Auswertungszeitraum der Meldewochen 40/2019 bis 11/2020 heranziehen (siehe dazu das PDF RKI – Influenza-Wochenbericht 2020-11, Seite 1):
Seit der 40. MW 2019 wurden insgesamt 165.036 labordiagnostisch bestätigte Influenzafälle an das RKI übermittelt. Bei 23.646 ( 14 %) Fällen wurde angegeben, dass die Patienten hospitalisiert waren. Es wurden bisher 412 Ausbrüche mit mehr als fünf Fällen an das RKI übermittelt, darunter 76 Ausbrüche in Krankenhäusern. Seit der 40. KW 2019 wurden insgesamt 265 Todesfälle mit Influenzavirusinfektion übermittelt. Die Grippewelle hat in Deutschland in der 2. KW 2020 begonnen und hält seitdem an.
Berechnet man das Verhältnis aus 165.036 Influenza-Fällen zu 265 Verstorbenen kommen wir auf einen Wert von 0,16. Ziehen wir nun diesen Wert zur Berechnung der Todeszahl für den Berichtszeitraum der Kalenderwoche 11/2020 heran, dann erhalten wir aus 127.263 Menschen mit dem Wert 0,16 203 Todesfälle aufgrund der Influenza-Viren.
Weil dieser Wert aufgrund des saisonalen Auftretens der Influenza ebenfalls nicht aussagekräftig ist, leiten wir aus 181.105 zu 127.262 Influenza-Fällen ein weiteres Verhältnis ab. Dies beträgt 70,3 und besagt, dass bis heute im Vergleich zum Vorjahr bereits 70% der Influenza-Einmeldungen erfolgt sind. Das heißt wir nutzen diese 70,3 um darüber den Verhältniswert des ganzen Jahres von 0,92 anteilig zu berechnen. Damit wird aus den 0,92 mittels der 70,3 ein Wert von 0,65. Dieser dient uns nun als Referenzwert zur Berechnung der Influenza-Toten im Berichtszeitraum des hier genutzten Influenza-Wochenberichts der Kalenderwoche 11/2020.
Mit den bereits erwähnten 127.263 Influenza-Fällen und den oben berechneten 0,65 ergibt sich die Zahl von 789 Influenza-Todesfällen.
Im täglichen Lagebericht des RKI zu Covid-19 vom 24. März 2020 sind 27.436 bestätigte Fälle, 114 Verstorbene und damit ein Verhältnis von 0,42 aufgeführt:

Lagebericht RKI 24-03-2020 – Bildquelle: Screenshot-Ausschnitt PDF
Setzt man nun die entsprechenden Werte in eine Tabelle ein, ergibt sich für den gleichen Berichtszeitraum folgendes Bild:
| Anzahl Infizierter | Todesfälle | Todesrate | |
| Covid-19 | 27.436 | 114 | 0,42 |
| Influenza | 127.263 | 789 | 0,65 |
Ausgehend von einem Mittelwert der Steigerungsrate der Covid-19-Ansteckungen von 30,54, der jedoch eine Standardabweichung von 22,36 bei einer Varianz von 499,75 beinhaltet, würden wir bereits am 29. März die gleiche Fallzahl an Covid-19-Erkrankten wie Influenza-Infizierten erreicht haben (125.063 zu 127.263). Siehe dazu auch die in den Quellen aufgeführte Berechnung Covid-19-Influenza.ods. Jedoch möchte ich an dieser Stelle auf Folgendes hinweisen:
Die Standardabweichung ist die Quadratwurzel aus der Varianz (Formel: Standardabweichung = √ Varianz). Die Standardabweichung ist ein Streuungsparameter, der anzeigt, inwieweit die Werte um den arithmetischen Mittelwert streuen; je größer die Standardabweichung (in Relation zum Mittelwert), desto größer die Streuung (und desto schlechter spiegelt der Mittelwert die Daten wider).
Das heißt, dass mit diesem Mittelwert de facto nicht gerechnet werden kann, um eine Aussage darüber zu treffen, wann eine identische Anzahl an Covid-19– und Influenza-Erkrankten vorliegt. Der einfachheithalber wollen wir jedoch diese Berechnung so durchführen (was die zugrunde liegende Argumentation eigentlich schwächt) und erhalten am „Gleichstandstag“ (also die Anzahl von Influenza– und Covid-19-Erkrankten ist an diesem Tag annähernd identisch) bei einer Sterberate von 0,42 den Wert von 525 Todefällen, die immer noch unter der der Influenza liegt.
Schlussbemerkung:
Ich weiß, dass dieser Herleitung schwierig zu folgen ist und ich hoffe zudem, dass ich keinen Denkfehler eingebaut habe. Sollte ich aber richtig liegen, zeigt es nur, dass die Gefahr bzgl. des Coronavirus, der die Covid-19-Erkrankung auslöst, weit weg von dem ihm unterstellten Horrorszenario liegt. Und damit kommen wir letztlich wieder zu dem immer anzustellenden Cui bono? Wem nutzt es?
Eine Frage, die ich in den letzten Artikeln und Videos zu beantworten versucht habe.
Ich bin gespannt auf eure Kommentare.
Quellen:
RKI – COVID-19 (Coronavirus SARS-CoV-2)
RKI – COVID-19: Fallzahlen in Deutschland und weltweit
RKI – Modellierung von Beispielszenarien der SARS-CoV-2-Epidemie 2020 in Deutschland
RKI – Influenza-Wochenbericht KW 11/2020
RKI – Täglicher Lagebericht 24.03.2020
RKI – Saisonberichte
RKI – Bericht zur Epidemiologie der Influenza in Deutschland Saison 2018/19
Worldometer – Covid-19
Worldometer – Covid-19 per 25. März 2020 als HTML-Sicherungsdatei
Berechnung Covid-19-Influenza.ods
Definition der Standardabweichung
Ein Artikel bildet zwangsweise die Meinung eines Einzelnen ab. In Zeiten der Propaganda und Gegenpropaganda ist es daher umso wichtiger sich mit allen Informationen kritisch auseinander zu setzen. Dies gilt auch für die hier aufbereiteten Artikel, die nach besten Wissen und Gewissen verfasst sind. Um die Nachvollziehbarkeit der Informationen zu gewährleisten, werden alle Quellen, die in den Artikeln verwendet werden, am Ende aufgeführt. Es ist jeder eingeladen diese zu besuchen und sich ein eigenes Bild mit anderen Schlussfolgerungen zu machen.
5 Antworten